Where the techniques of Maths
are explained in simple terms.
Trigonometric functions - Integration - Applications finding areas.
Test Yourself 1.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
Solve the following problems as indicated:
| Area - 1 curve |
1. Find the area between y = 3sin 2x and the x-axis between x = 0 and x = π. Answer:Area = 6 u2. |
2. (i) Sketch the curve y = 2cos 2x + 1 between x = 0 and x = π/2 showing the intercepts on the axes.
(ii) Find the exact area between the curve |
| 3. Find the area between the curve y = 2sec2x and the x-axis between x = 0 and x = π/4. Answer:Area = 2 u2. |
4. For the function f(x) = 2cos x + 1,
|
|
| 5. (i) Sketch the curve y = -1 - sin 3x between x = 0 and x = π. (ii) Find the area enclosed between the curve and the x axis between x = 0 and |
6. The diagram below shows the graph of y = cos 2x + sin x.
Calculate the exact area between the curve and the x axis from x = -π/2 to π/2. Answer:Area = (3√3)/2 u2. |
|
7. If f(x) = (1 + tan x)2 for 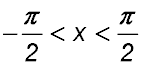 . .
Answer:(i) At x = -π/4. (ii) min TP at (-π/4, 0). (iv) Area = 2 u2 |
8. The breathing cycle for an adult at rest takes 5 seconds on average. For the first 2.5 seconds (0 < t ≤ 2.5), breath is taken into the lungs. For the remaining 2.5 seconds (2.5 < t ≤ 5), breath is exhaled. The rate (R litres/second) at which breath is being inhaled into or exhaled from the lungs at time t through the 5 second cycle can be modelled by the equation
How many litres of air is inhaled into the lungs during one breathing cycle? |
|
| Area - 2 curves with no point of intersection. |
9. (i) Sketch the graphs of y = sec2 x and y = x for 0 ≤ x ≤ π/4.
Answer:Area = 1 - π2/32. |
10. (i) Sketch the graphs of x = sec2 x and y = cos x for [0 , π/2].
(ii) Find the area between the two curves within the domain [0, π/3]. Answer:Area = √3 /2 u2. |
| Area - 2 curves with one point of intersection |
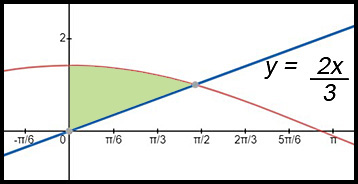
11. The diagram shows the curves 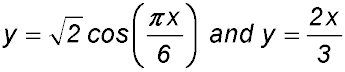 . .
(i) Show that the point of intersection has coordinates (1.5, 1). (ii) Find the exact area described the the y axis and the area between the two curves up their point of intersection.
|
|
12. 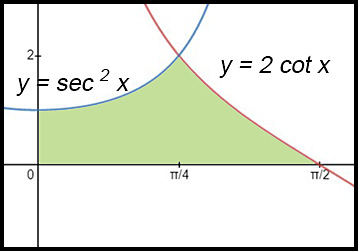
The diagram shows the region bounded by the curves y = sec2 x, y = 2 cot x and the coordinate axes. Answer:(iii) Area = 1 + ln2 u2. |
||
| 13. (i) Sketch the graphs of y = sin 2x and y = 3 cos x in the domain 0 ≤ x ≤ π.
(ii) Find the area bounded between the two curves in the given domain. Answer:Area = 4 u2. |
||
14. (i) Sketch the curves y = sin 2x and y = cos x in the domain [-π/2, π/2]. (ii) fine the total area enclosed by these two curves in the given domain. Answer:Area = 1.5 u2. |
||
| Area - 2 curves with two points of intersection |
15. 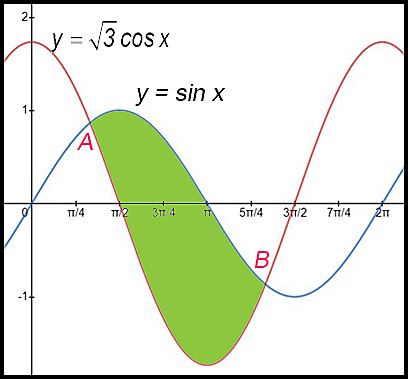
The diagram above shows the graphs of y = sin x and y = √3 cos x (0 ≤ x ≤ 2π). The graphs intersect at points A and B. Answer:(iii) Area = 4 u2. |
|
| 16. (i) Show that the curves y = sec 2x - 1 and y = sin 2x intersect at x = 0 and at x = 0.896 (correct to 3 decimal places). Draw a rough sketch if this helps. (ii) Find the area between these two curves between the two points of intersection |
||

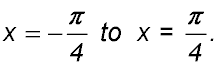
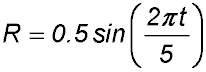
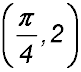 lies on both y = sec2 x
lies on both y = sec2 x